OBS: Comentários feito por professores da instituição.
Questão - 22
Click na imagem para visualizá-la melhor!

O consumo dessas pastilhas de iodeto de potássio pode diminuir a incidência de tumores na seguinte glândula:
(A) tireoide
(B) hipófise
(C) pâncreas
(D) suprarrenal
Alternativa correta: (A)
Eixo interdisciplinar: Os Seres Vivos e sua Relação com o Ambiente
Item do programa: Sistemas vitais dos animais e vegetais
Subitem do programa: Sistemas de integração
Objetivo: Identificar a glândula endócrina com concentração do íon iodeto para a produção de seu hormônio.
Comentário da questão:
A glândula tireoide concentra o íon iodeto e o incorpora em seus hormônios tri-iodotironina e tiroxina.
Em acidentes nucleares, um dos radioisótopos liberados é o iodeto radioativo, que, ao ser incorporado pela tireoide, pode acarretar o aparecimento de tumores malignos nessa glândula. O uso de pastilhas contendo iodeto não radioativo visa a diluir o radiosótipo, evitando grandes concentrações de radioatividade na tireoide.
Percentual de acertos: 70,36%
Nível de dificuldade: Fácil (acima de 70%)
Questão - 23
Click na imagem para visualizá-la melhor!

Suponha que, em alguns dos locais atingidos pela radiação, as pastilhas disponíveis continham, cada uma, 5 x 10−4 mol de iodeto de potássio, sendo a dose prescrita por pessoa de 33,2 mg por dia. Em razão disso, cada pastilha teve de ser dissolvida em água, formando 1L de solução.
O volume da solução preparada que cada pessoa deve beber para ingerir a dose diária prescrita de iodeto de potássio corresponde, em mililitros, a:
(A) 200
(B) 400
(C) 600
(D) 800
Alternativa correta: (B)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Soluções
Subitem do programa: Unidades de concentração (em g.L-1 e em quantidade de matéria)
Objetivo: Calcular o volume de uma solução com base em uma dose prescrita de iodeto de potássio.
Comentário da questão:
A massa molar do iodeto de potássio (KI) é igual a soma das massas molares do potássio e do iodo:
39 + 127 = 166 g
Sabendo que uma pastilha prescrita contém 5 x 10-4 mol de KI, pode-se calcular a massa de KI presente em cada uma:
1 mol -> 166 g
5 x 10-4 mol -> X
X = 0,083 g = 83 mg
Como essa foi a quantidade de massa de KI dissolvida, a concentração de 1 L de solução formada é igual a 83 mg.L-1.
O volume de solução que contém 33,2 mg de KI corresponde a:
83 mg -> 1 L
33,2 mg -> Y
Y = 0,4 L = 400 mL
O volume de solução a ser ingerido é igual a 400 mL.
Percentual de acertos: 43,10%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 24
Click na imagem para visualizá-la melhor!

Alternativa correta: (A)
Eixo interdisciplinar: Bases Metodológicas e Instrumentais
Item do programa: Sucessões
Subitem do programa: Progressões aritméticas e geométricas
Objetivo: Calcular o termo geral de uma progressão geométrica.
Comentário da questão:
No instante inicial t0 = 0, a massa do radioisótopo é igual a .

Após um período de tempo igual a uma meia-vida, tem-se:
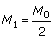
Após um período de duas meias-vidas:

Observa-se, assim, que a massa diminui segundo uma P.G. de razão 1/2 , cujo termo geral é dado por:

sendo n o número de meias-vidas.
Como a meia-vida do radioisótopo é igual a 20 h, para um período de tempo correspondente a 5 meias-vidas (100 h), a massa do radioisótopo será cerca de:
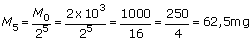
Percentual de acertos: 45,49%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 25
Click na imagem para visualizá-la melhor!

O gráfico que representa o hormônio progesterona, em um ciclo menstrual normal, está indicado pela seguinte letra:
(A) W
(B) X
(C) Y
(D) Z
Alternativa correta: (A)
Eixo interdisciplinar: Os Seres Vivos e sua Relação com o Ambiente
Item do programa: Sistemas vitais dos animais e vegetais
Subitem do programa: Sistemas de integração
Item do programa 2: Sistemas vitais dos animais e vegetais
Subitem do programa 2: Reprodução
Objetivo: Descrever a produção do hormônio progesterona durante o ciclo menstrual normal.
Comentário da questão:
A progesterona é produzida pelo corpo lúteo, formado após a ovulação, que ocorre em torno do 14º dia do ciclo menstrual normal. Dessa forma, os níveis de progesterona aumentam na segunda fase do ciclo, mas voltam a diminuir no final dele, com o desaparecimento do corpo lúteo. Essa concentração hormonal pode ser representada graficamente da seguinte forma:

Percentual de acertos: 32,27%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 26

lternativa correta: (C)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Funções químicas
Subitem do programa: Classificação e nomenclatura das substâncias orgânicas
Objetivo: Discriminar o ácido carboxílico presente em maior quantidade em uma amostra de manteiga.
Comentário da questão:
A partir do gráfico, constata-se que o éster formado em maior quantidade tem fórmula molecular C8H16O2.
Esse éster é formado pela reação entre um ácido carboxílico e o etanol, cuja fórmula molecular é C2H6O. Essa reação pode ser representada pela seguinte equação:

Percentual de acertos: 14,37%
Nível de dificuldade: Difícil (abaixo de 30%)
Questão 27
Um soldado fez n séries de flexões de braço, cada uma delas com 20 repetições. No entanto, como consequência das alterações da contração muscular devidas ao acúmulo de ácido lático, o tempo de duração de cada série, a partir da segunda, foi sempre 28% maior do que o tempo gasto para fazer a série imediatamente anterior. A primeira série foi realizada em 25 segundos e a última em 1 minuto e 40 segundos.
Considerando log 2 = 0,3, a soma do número de repetições realizadas nas n séries é igual a:
(A) 100
(B) 120
(C) 140
(D) 160
Alternativa correta: (C)
Eixo interdisciplinar: Bases Metodológicas e Instrumentais
Item do programa: Sucessões
Subitem do programa: Progressão geométrica
Objetivo: Calcular o número de elementos de um conjunto com base em propriedades dos logaritmos.
Comentário da questão:
A primeira série foi feita em 25 segundos, e cada série seguinte teve um aumento de 28% em relação ao tempo gasto na série imediatamente anterior. Os tempos gastos para fazer as n séries formam uma progressão geométrica com os seguintes termos:

Percentual de acertos: 36,00%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 28
No interior do casco dos navios, existem tanques que podem ter seu volume preenchido parcial ou totalmente com água do mar em função das necessidades de flutuabilidade.
Como os tanques são constituídos de materiais metálicos, eles sofrem, ao longo do tempo, corrosão pelo contato com a água do mar, conforme a equação:

Um processo corrosivo no interior de um tanque fechado apresenta as seguintes características:

Admita que, durante todo o processo de corrosão, o ar no interior do tanque esteve submetido às CNTP, com comportamento ideal, e que apenas o oxigênio presente no ar foi consumido.
A massa de ferro, em quilogramas, consumida após o processo corrosivo foi igual a:
(A) 1300
(B) 1600
(C) 2100
(D) 2800
Alternativa correta: (B)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Gases ideais
Subitem do programa: Transformações e misturas gasosas
Item do programa 2: Cálculo estequiométrico simples
Subitem do programa 2: Quantidade de matéria, massa e volume nas condições normais
Objetivo: Calcular a massa de ferro consumida em um processo corrosivo.
Comentário da questão:
A variação da concentração percentual de gás oxigênio no interior do tanque ao longo do processo corrosivo corresponde a:
20,9 - 19,3 = 1,6%
O volume de oxigênio consumido no processo de corrosão do ferro consiste em 1,6% do volume de ar no interior do tanque. Logo:

Percentual de acertos: 37,34%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 29
O aumento da poluição atmosférica, especialmente pelo acúmulo de gases do efeito estufa, como o CO2, tem acarretado a elevação da temperatura global. Alguns seres vivos, no entanto, apresentam um metabolismo capaz de fixar esse gás em matéria orgânica.
Em condições ideais, o grupo de organismos com maior capacidade de fixar CO2 é:
(A) levedo
(B) bactéria
(C) zooplâncton
(D) fitoplâncton
Alternativa correta: (D)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Transformações energéticas nos seres vivos
Objetivo: Identificar grupo de organismos com maior capacidade de fixação de CO2.
Comentário da questão:
Dentre os tipos de organismos citados, o fitoplâncton é o único com capacidade de fixar o CO2 em matéria orgânica através do processo fotossintético.
Percentual de acertos: 49,89%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 30
Em uma das etapas do ciclo de Krebs, ocorre uma reação química na qual o íon succinato é consumido. Observe a fórmula estrutural desse íon:

Na reação de consumo, o succinato perde dois átomos de hidrogênio, formando o íon fumarato. Sabendo que o íon fumarato é um isômero geométrico trans, sua fórmula estrutural corresponde a:
Click na imagem para visualizá-la melhor!

Alternativa correta: (D)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Funções químicas
Subitem do programa: Classificação e nomenclatura das substâncias orgânicas; isomeria
Objetivo: Identificar a fórmula estrutural espacial do íon fumarato.
Comentário da questão:
O íon fumarato é formado a partir da remoção de dois átomos de hidrogênio do succinato. A perda de dois átomos de hidrogênio acarreta a formação de uma ligação dupla. Com base nestas informações, e sabendo que o íon fumarato é um isômero geométrico trans, sua fórmula estrutural espacial corresponde a:

Percentual de acertos: 46,77%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 31
Uma família comprou água mineral em embalagens de 20 L, de 10 L e de 2 L. Ao todo, foram comprados 94 L de água, com o custo total de R$ 65,00.
Veja na tabela os preços da água por embalagem:

Nessa compra, o número de embalagens de 10 L corresponde ao dobro do número de embalagens de 20 L, e a quantidade de embalagens de 2 L corresponde a n.
O valor de n é um divisor de:
(A) 32
(B) 65
(C) 77
(D) 81
Alternativa correta: (C)
Eixo interdisciplinar: Bases Metodológicas e Instrumentais
Item do programa: Sistemas de equações
Subitem do programa: Lineares
Objetivo: Calcular o número de elementos de um conjunto com base em sistemas lineares.
Comentário da questão:
Considere x, y e z, respectivamente, o número de embalagens de 20 L, 10 L e 2 L compradas pela família. Assim, pode-se escrever:

Para resolver esse sistema linear, substitui-se y por 2x nas duas primeiras equações:

O número 7 é divisor de 77.
Percentual de acertos: 40,13%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 32
Durante o processo evolutivo, algumas organelas de células eucariotas se formaram por endossimbiose com procariotos. Tais organelas mantiveram o mesmo mecanismo de síntese proteica encontrado nesses procariotos.
Considere as seguintes organelas celulares, existentes em eucariotos:
1 - mitocôndrias
2 - aparelho golgiense
3 - lisossomas
4 - cloroplastos
5 - vesículas secretoras
6 - peroxissomas
Nas células das plantas, as organelas que apresentam o mecanismo de síntese proteica igual ao dos procariotos correspondem às de números:
(A) 1 e 4
(B) 2 e 3
(C) 3 e 6
(D) 4 e 5
Alternativa correta: (A)
Eixo interdisciplinar: Os Seres Vivos e sua Relação com o Ambiente
Item do programa: A célula
Subitem do programa: Estruturas e organelas celulares e suas funções
Objetivo: Identificar organelas celulares de eucariotos originadas de endossimbiose com procariotos.
Comentário da questão:
Nas mitocôndrias e nos cloroplastos das plantas, observa-se um mecanismo de síntese proteica similar ao encontrado em procariotos, de onde se conclui que tais organelas se formaram pelo processo de endossimbiose durante a evolução. Os eucariotos formados em consequência desse processo passaram a ter maior eficiência em seus sistemas de transformação energética.
Percentual de acertos: 47,89%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 33
Click na imagem para visualizá-la melhor!

Considere um experimento em que uma enzima, cuja constante de Michaelis é igual a 9 x 10−3 milimol/L, foi incubada em condições ideais, com concentração de substrato igual a 10−3 milimol/L. A velocidade de reação medida correpondeu a 10 unidades. Em seguida, a concentração de substrato foi bastante elevada de modo a manter essa enzima completamente saturada.
Neste caso, a velocidade de reação medida será, nas mesmas unidades, equivalente a:
(A) 1
(B) 10
(C) 100
(D) 1000
Alternativa correta: (C)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Cinética reacional
Subitem do programa: Reações enzimáticas
Objetivo: Calcular a velocidade de reação de uma enzima.
Comentário da questão:
Sabe-se que a velocidade máxima de reação é atingida quando uma enzima atua sobre um excesso de substrato, ou seja, quando está completamente saturada por ele.
Dada a equação de Michaelis, a Vmax pode ser calculada em qualquer condição de concentração de substrato. Dessa forma:

Como a concentração de substrato foi elevada de modo a manter a enzima completamente saturada, a velocidade de reação na segunda parte do experimento será igual à velocidade máxima. Logo:
v = 100
Percentual de acertos: 39,51%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 34
Um cliente, ao chegar a uma agência bancária, retirou a última senha de atendimento do dia, com o número 49. Verificou que havia 12 pessoas à sua frente na fila, cujas senhas representavam uma progressão aritmética de números naturais consecutivos, começando em 37.
Algum tempo depois, mais de 4 pessoas desistiram do atendimento e saíram do banco. Com isso, os números das senhas daquelas que permaneceram na fila passaram a formar uma nova progressão aritmética.
Se os clientes com as senhas de números 37 e 49 não saíram do banco, o número máximo de pessoas que pode ter permanecido na fila é:
(A) 6
(B) 7
(C) 9
(D) 12
Alternativa correta: (B)
Eixo interdisciplinar: Bases Metodológicas e Instrumentais
Item do programa: Sucessões
Subitem do programa: Progressão aritmética
Objetivo: Calcular o número de elementos de um conjunto com base no conceito de progressão aritmética.
Comentário da questão:
A sequência formada pelos números das senhas das pessoas que estavam na fila, incluindo a do último cliente que chegou ao banco, correspondia à seguinte progressão aritmética:
(37, 38, 39......, 49)
Após a desistência de algumas pessoas, formou-se a seguinte P.A., de razão R e número de termos n:
(37, a2, a3, a4, ... , 49)

A P.A. tem menos de 13 elementos. Assim, para o valor de n ser máximo, R deve ser igual a 2.
Logo, n = 7.
Percentual de acertos: 42,87%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 35

O número máximo de lâmpadas que podem ser mantidas acesas corresponde a:
(A) 10
(B) 15
(C) 20
(D) 30
Alternativa correta: (C)
Eixo interdisciplinar: A Matéria em Equilíbrio e em Movimento
Item do programa: Fenômenos elétricos
Subitem do programa: Lei de Ohm, circuitos elétricos, energia e potência elétrica
Objetivo: Calcular potência máxima consumida por lâmpadas em paralelo.
Comentário da questão:
A potência máxima que pode ser consumida pelas lâmpadas do circuito corresponde ao produto entre a tensão eficaz e a corrente máxima permitida pelo fusível. Logo:

Como a potência PL consumida por apenas uma dessas lâmpadas, sob a tensão de 120 V, é de 60 W, o número máximo n de lâmpadas que podem ser mantidas acesas é igual a:

Percentual de acertos: 57,92%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 36

A resistência equivalente, em ohms, de apenas 8 lâmpadas acesas é cerca de:
(A) 30
(B) 60
(C) 120
(D) 240
Alternativa correta: (A)
Eixo interdisciplinar: A Matéria em Equilíbrio e em Movimento
Item do programa: Fenômenos elétricos
Subitem do programa: Lei de Ohm, circuitos elétricos, energia e potência elétrica
Objetivo: Calcular a resistência equivalente de um circuito.
Comentário da questão:
A relação entre a resistência, a tensão e a potência para cada lâmpada pode ser expressa da seguinte forma:

Sendo V = 120 V e PL = 60 W, tem-se:

Como as 8 lâmpadas são idênticas, a resistência equivalente dessa associação em paralelo será:
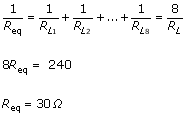
Percentual de acertos: 26,62%
Nível de dificuldade: Difícil (abaixo de 30%)
Questão - 37
Click na imagem para visualizá-la melhor!

Alternativa correta: (B)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Funções químicas
Subitem do programa: Classificação das substâncias inorgânicas
Item do programa 2: Equilíbrio químico
Subitem do programa 2: Acidez e alcalinidade
Objetivo: Identificar soluto para preparo de solução fisiológica salina com pH neutro.
Comentário da questão:
Dissolvendo-se as substâncias disponíveis no laboratório em água, chega-se às seguintes conclusões:

Percentual de acertos: 51,75%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 38
Click na imagem para visualizá-la melhor!

Alternativa correta: (D)
Eixo interdisciplinar: A Matéria em Equilíbrio e em Movimento
Item do programa: Leis de Newton
Subitem do programa: Dinâmica e cinemática dos movimentos uniforme e uniformemente variado
Objetivo: Transferir conhecimentos acerca das leis de Newton para o cálculo de tempo em queda livre.
Comentário da questão:
De acordo com as leis de Newton e com a equação horária do movimento uniformemente variado, a altura H e o tempo de queda tq de um corpo sob a ação da gravidade g são relacionados de acordo com a seguinte equação:
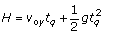
sendo voy a componente vertical da velocidade inicial.
Como o lançamento é horizontal, voy = 0. Logo, o tempo de queda só depende da altura.
Portanto, como todas as bolas são lançadas da mesma altura, com componentes verticais da velocidade inicial nulas, o tempo de queda será igual nos 3 lançamentos:

Percentual de acertos: 23,23%
Nível de dificuldade: Difícil (abaixo de 30%)
Questão - 39
Click na imagem para visualizá-la melhor!

Alternativa correta: (C)
Eixo interdisciplinar: A Matéria em Equilíbrio e em Movimento
Item do programa: Leis de Newton
Subitem do programa: Dinâmica e cinemática dos movimentos uniforme e uniformemente variado
Objetivo: Transferir conhecimentos acerca das leis de Newton para cálculo de alcance de um corpo lançado de uma dada altura.
Comentário da questão:
De acordo com as leis de Newton, o alcance A de um corpo lançado horizontalmente de uma altura H, sob a ação da gravidade g, corresponde à seguinte relação:

sendo vox a componente da velocidade inicial paralela ao solo.
Como todas as bolas são lançadas da mesma altura, o alcance será proporcional ao valor da componente da velocidade inicial paralela ao solo.De acordo com a tabela apresentada, a relação entre as componentes de velocidade inicial paralela ao solo é dada por:

Logo:
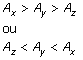
Percentual de acertos: 50,17%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 40
Click na imagem para visualizá-la melhor!

Alternativa correta: (D)
Eixo interdisciplinar: Os Constituintes Fundamentais da Matéria
Item do programa: Bases moleculares da vida
Subitem do programa: Ácidos nucleicos, proteínas, lipídios, glicídios, aminoácidos e nucleotídeos
Eixo interdisciplinar 2: Os Seres Vivos e sua Relação com o Ambiente
Item do programa 2: As bases da genética
Subitem do programa 2: Genes e código genético
Objetivo: Identificar o aminoácido introduzido em uma proteína após a mutação de uma base nitrogenada.
Comentário da questão:
Sabendo que a metionina introduzida pelo códon iniciador AUG foi removida, restaram as seguintes bases que codificavam a proteína sintetizada pelo RNA mensageiro original:
GCUAAAUUAGAC...
Esta sequencia de bases corresponde aos seguintes aminoácidos: alanina, lisina, leucina e aspártico. Na célula mutante, o código UUA do terceiro aminoácido (leucina) transformou-se em UUU. Portanto, o terceiro aminoácido da estrutura primária da proteína mutante passou a ser a fenilalanina.
Percentual de acertos: 45,19%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 41

Alternativa correta: (D)
Eixo interdisciplinar: As Substâncias e suas Transformações
Item do programa: Equilíbrio químico
Subitem do programa: O estado de equilíbrio e suas perturbações
Objetivo: Discriminar alteração em um sistema geradora de maior consumo de monóxido de carbono.
Comentário da questão:
Para reduzir a concentração de monóxido de carbono (CO) no processo, o equilíbrio químico deve ser deslocado no sentido de consumi-lo, ou seja, da esquerda para a direita.

De acordo com o princípio de Le Chatelier, quando se aumenta a pressão no interior de um sistema, o equilíbrio é deslocado no sentido de menor volume. Como os reagentes ocupam 3 volumes em relação aos 2 volumes ocupados pelo produto, com o aumento da pressão, o equilíbrio químico será deslocado no sentido direto.
Assim, para se reduzir a concentração de CO, deve-se aumentar a pressão.
Percentual de acertos: 29,08%
Nível de dificuldade: Difícil (abaixo de 30%)
Questão - 42
rês modelos de aparelhos de ar-condicionado, I, II e III, de diferentes potências, são produzidos por um determinado fabricante.
Uma consulta sobre intenção de troca de modelo foi realizada com 1000 usuários desses produtos. Observe a matriz A , na qual cada elemento aij representa o número daqueles que pretendem trocar do modelo i para o modelo j.

Escolhendo-se aleatoriamente um dos usuários consultados, a probabilidade de que ele não pretenda trocar seu modelo de ar-condicionado é igual a:
(A) 20%
(B) 35%
(C) 40%
(D) 65%
Alternativa correta: (B)
Eixo interdisciplinar: Bases Metodológicas e Instrumentais
Item do programa: Problemas de contagem
Subitem do programa: Cálculo de probabilidades
Item do programa 2: Matrizes
Subitem do programa 2: Representações
Objetivo: Calcular uma probabilidade com base na leitura de uma matriz.
Comentário da questão:
Cada elemento aij da matriz representa o número de pessoas que pretendem trocar do modelo i para o modelo j.
Na matriz, os elementos a11, a22, a33, que compõem uma diagonal, representam a quantidade de pessoas que não pretendem trocar de modelo, tendo em vista que i é igual j.
Então:
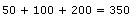
Como foi consultado um total de 1000 usuários, a probabilidade P de que um deles não pretenda trocar seu modelo de ar-condicionado é igual a:

Percentual de acertos: 47,43%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)
Questão - 43
Click na imagem para visualizá-la melhor!


Percentual de acertos: 53,25%
Nível de dificuldade: Médio (acima de 30% e igual ou abaixo de 70%)